In Particle-driven Wakefield Accelerators (PWFA) the plasma wave is excited by the space charge forces of the driving electron bunch that displace the plasma electrons creating high gradient accelerating fields between the local depleted and enriched plasma electron densities. In that way the driving electron pulse can transfer a large fraction of its kinetic energy to a subsequent bunch (witness bunch) placed at a proper distance.
The accelerating field scaling law
$\large{E_{acc}\left[ MV/m\right] = 244 \frac{N_b}{2 \times 10^{10}}\left( \frac{600}{\sigma_z[\mu m]}\right)^2}$
shows that high charge ($N_b$) and short bunch length ($\sigma_z$) play an essential role in achieving ultra-high gradients. For example with a beam of $N_b = 2 \times 10^{10}$ particles (corresponding to $\sim 3.2 \, nC$) and $\sigma_z= 20\, \mu m$, accelerating gradients of the order of $100 \, GV/m$ can be driven in a plasma with a density of $10^{17} \, cm^{-3}$. Moreover since the dependence on the bunch length is inverse quadratic, more challenging accelerating gradients of the order of $1 \, TV/m$ could be obtained with shorter bunches: $\sigma_z = 0.8\, \mu m$ and $N_b = 10^8$ (corresponding to $\sim 20 \, pC$), in a plasma with a density of $7 \times 10^{19} \, cm^{-3}$.
There are several possible PWFA scenarios when operating such experiments, mainly depending on the working regime (linear or nonlinear). The linear regime, where the bunch density is very small compared to the plasma, has the advantage that the plasma oscillation may be resonantly driven, but has the notable drawback that the focusing is nonlinear in radial coordinate and the same dependence would apply for the provided acceleration. In the nonlinear regime, called blow-out regime [1], the beam density is much greater than the plasma density (nb >> np) and the beam channel is completely rarefied of plasma electrons. Under these conditions the plasma response is very nonlinear, the plasma wavelength λp depends on the wakefield amplitude and large wave-breaking spikes are excited at the end of the first plasma oscillation.
To overcome these limitations, the beam driven experiment at SPARC LAB, named “COMB”, will operate in the so-called quasi-nonlinear regime [2]. It requires operations where one uses beam with relatively low charge and longitudinal and transverse beam size smaller than a plasma wavelength, σr, σz << λp ~ 200 µm. In this case, the beam density may exceed that of the plasma, producing blowout (strongly non linear regime) [3], but due to the small total charge, producing a disturbance that behaves in many ways as linear, having frequency essentially that of linear plasma oscillations.
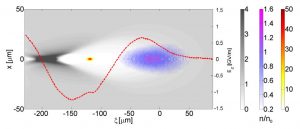
Accelerating scheme structure. As we can see the driver has a low density (purple scale) and the witness has a very high density (orange scale). The field is reported in red. We can notice the flattening in correspondence of the trailing bunch position

Permanent magnet quadrupole
The reduction of the bunch transverse dimensions to match the desired beam density requires a proper focusing system. Such a task cannot be accomplished with normal-conducting electromagnetic solenoids or quadrupoles because the provided field gradients would be too weak. In this context the state of the art is represented by permanent-magnet quadrupoles (PMQ) [4]. So far, field gradients of about 560 T/m have been reported when using small-bore PMQs manufactured with neodymium–iron–boride (NdFeB) materials. Another promising way to focus the beam is to use an active plasma lens [5], where the discharge that ionize the plasma act as the focusing element. The field gradients available by plasma lenses are in the order of kT/m, thus requiring even less space than PMQ to focus the beam. More information are available on the plasma lens page.
In a PWFA driven by a single electron bunch, the peak accelerating field is, in principle, limited to twice the value o the peak decelerating field within the bunch (transformer ratio R=2). Therefore the maximum possible energy gain for a trailing bunch is less than twice the incoming energy. Several methods has been proposed to increase the accelerating field. A very promising method is the so called ramped bunch train and consists of using a train of $N_T$ equidistant bunches wherein the charge increases along the train producing an accelerating field resulting in a transformer ratio proportional to the number of driving bunches. For this application, it is essential to create trains of high-brightness femtosecond long microbunches with stable and adjustable length, charge, and spacing.
A lot of efforts are now ongoing worldwide to produce the required bunch train configurations. The method we propose to achieve the required bunch train quality is based on the so called Laser Comb Technique [6] that we have proposed some year ago and which has been tested with the SPARC photoinjector [7]. In this injector operating mode, the photocathode is illuminated by a comb-like laser pulse in order to produce a train of sub-picosecond high-charge density electron bunches within the same RF gun accelerating bucket. Downstream of the gun exit, the work done by the space charge force produces a linear energy chirp along each pulse, which can be exploited to compress the initial charge profile with an RF accelerating structure, operating in the velocity bunching mode [8].
With such a train of $N_T$ bunches a resonant excitation of plasma waves can be performed with a convenient scaling with $N_T$ in the accelerating field:
$\large{E_{acc}\left[ MV/m\right] = 244 \frac{N_b}{2 \times 10^{10}}\left( \frac{600}{\sigma_z[\mu m]}\right)^2 \times N_T^2}$
For example train of 4 bunches with 16 pC/bunch separated by one plasma wavelength (160 µm), propagating in a plasma of density 3 1022 particles/m3 can generate an accelerating field in excess of 3 GV/m.
Useless to mention that electron pulse trains with some hundreds pC charge, a sub-picosecond length and a repetition rate of some terahertz can be useful also to drive pump and probe or multi-color free-electron laser (FEL) experiments, generation of narrow-band terahertz radiation [9] and to drive Dielectric Wake Field Acceleration (DWFA) experiments [10].
Publication highlights
- “Laser comb with velocity bunching: Preliminary results at SPARC”, M. Ferrario et al., Nucl. Instrum. Meth. Phys. Res. A vol. 637 (2011) pag. S43, doi: 10.1016/j.nima.2010.02.018
- “Beam manipulation with velocity bunching for PWFA applications”, R. Pompili et al., Nucl. Instrum. Meth. Phys. Res. A vol. 829 (2016) pag. 17, doi: 10.1016/j.nima.2016.01.061
- “Focusing of High-Brightness Electron Beams with Active-Plasma Lenses”, R. Pompili et al., Phys. Rev. Lett. vol. 121 (2018) pag. 174801, doi: 10.1103/PhysRevLett.121.174801
- “Energy spread minimization in a beam-driven plasma wakefield accelerator”, R. Pompili et al., Nature Phys. vol. 17 (2021) pag 499, doi: 10.1038/s41567-020-01116-9
- “First emittance measurement of the beam-driven plasma wakefield accelerated electron beam”, V. Shpakov et al., Phys. Rev. Accel. Beams vol. 24 (2021) pag. 051301, doi: 10.1103/PhysRevAccelBeams.24.051301
- “Free-electron lasing with compact beam-driven plasma wakefield accelerator”, R. Pompili et al., Nature vol. 605 (2022) pag 659, doi: 10.1038/s41586-022-04589-1
- “Stable Operation of a Free-Electron Laser Driven by a Plasma Accelerator”, M. Galletti et al., Phys. Rev. Lett. vol. 129 (2022) pag 234801, doi:10.1103/PhysRevLett.129.234801
- “Progress towards demonstration of a plasma-based FEL”, E. Chiadroni, Proceedings of 13th IPAC (2022), pag. MOPLXGD2, doi: 10.18429/JACoW-IPAC2022-MOPLXGD2
- “Experimental observation of the transition between hose and self-modulation instability regimes”, A. Del Dotto et al., Phys. Plasmas vol. 29 (2022), pag. 100701, doi: 10.1063/5.0093769
- “Plasma acceleration-induced betatron radiation: a potential seed for Free Electron Lasers”, A. Ghigo et al., Proceedings of 14th IPAC (2023), pag. TUPL049, doi
- : 10.18429/JACoW-IPAC2023-TUPL049
- “Beam dynamics optimization for high gradient beam driven plasma wakefield acceleration at SPARC-LAB”, M. Carillo et al, J. Phys.: Conf. Ser. vol. 2687 (6) (2024) pag. 062023, doi: 10.1088/1742-6596/2687/6/062023
- “Acceleration and focusing of relativistic electron beams in a compact plasma device”, R. Pompili et al., Phys. Rev. E vol. 109 (2024) pag. 055202, doi: 10.1103/PhysRevE.109.055202
- “Recovery of hydrogen plasma at the sub-nanosecond timescale in a plasma-wakefield accelerator”, R. Pompili et al., Comm. Phys., vol. 7 (2024) pag 241, doi: 10.1038/s42005-024-01739-x
- “Experimental observation of space-charge field screening of relativistic particle bunch in plasma”, L. Verra et al., Phys. Rev. Lett., vol. 133 (2024) pag 035001, doi: 10.1103/PhysRevLett.133.035001
- “Study of the transfer and matching line for a PWFA-driven FEL”, P. Iovine et al., J. Phys.: Conf. Ser. vol. 2687 (2024), pag. 042004, doi: 10.1088/1742-6596/2687/4/042004
- “Prospects for free-electron lasers powered by plasma-wakefield-accelerated beams”, M. Galletti et al., Nature Photonics, vol. 18 (2024) pag. 780, doi: 10.1038/s41566-024-01474-3
Plasma experiments

