In LWFA, the ponderomotive force of a laser pulse, traveling through an under-dense plasma, can excite a plasma wave with longitudinal electric fields larger than 10 GV/m. Electrons can then be accelerated up to ultra-relativistic energies on a centimeter scale. Terawatt-class lasers are needed in order to provide the required electric field.
We are planning, in our external injection project “EXIN”, to transport ultra-short electron bunches (<20 fs) and ultra-intense laser pulses (>1018 W cm-2), generated by the SPARC photo-injector in velocity bunching and by the FLAME laser in a synchronized fashion at the tens of fs level, in an hydrogen filled glass capillary, in order to perform acceleration of the electron bunch by a plasma wave driven by the laser pulse. The main aim of this experiment is to demonstrate that a high brightness electron beam can be accelerated by a plasma wave without any significant degradation of its quality. A 10 pC electron bunch, 10 fs long will be produced by the linac and transported to injection into the capillary, which is 100 micron wide, at a gas density around 1017 cm-3 . The laser pulse, 25 fs long, focused down to 65 microns into the capillary will be injected ahead of the bunch, and will drive a weakly non-linear plasma wave with wavelength of about 130 microns. A proper phasing of the two pulses allows acceleration of electrons from the injection energy of 150 MeV up to about 570 MeV for a 8 cm long capillary.
The route to external injection experiment can be divided into two parts. The first one concerns the generation and acceleration of proper high brightness electron beam up to the injector end. The second part consists in the design, realization and commissioning of the transport line down to the interaction chamber with the plasma wave and the subsequent diagnostic stations. Moreover, studies for designing the high power laser pulse transport line are underway and partially tested during the Thomson experiment. For each part, the planned activities are similar: after intensive numerical simulations to fix the machine working points, all the sub-systems (e.g. timing, diagnostics, beam transport, etc.) will be installed and tested independently, whenever possible, and eventually the whole accelerator will be commissioned. The main goal is to produce in a stable and reproducible way a beam with a charge up to 25 pC, an energy up to 1 GeV with a spread less than 1% and a normalized emittance of few mm-mrad.
High accuracy and precision diagnostic tools are compulsory for both transverse and longitudinal characterization of the electron beam; preferably non intercepting and single shot diagnostics should provide the required resolution of few tens of fs bunch length and few microns transverse beam size. At SPARC LAB a wide energy range spectrometer will provide means of measuring the beam energy and its spread. The emittance will be measured by the quadrupole scan technique, tough, if the beam energy spread is relatively large, the results could be unreliable due to chromatic effects. As for the longitudinal diagnostics, we plan to insert an RF deflector downstream the plasma interaction chamber. Moreover, since the same line and interaction chamber will be used to perform PWFA experiments, we will profit of the non intercepting, longitudinal diagnostic tool which is the Electron Optical Sampling. Finally, a device to measure the betatron radiation and the coherent transition radiation is foreseen.
The high brightness beam length $\sigma_z$, needed to feed the plasma wave, must be short compared to the plasma wavelength λp (λp > (30 – 40) $\sigma_z$), in order to prevent an excessive energy spread after plasma interaction. Plasma wave regimes can range from linear to highly non-linear: generally speaking, the first are more stable but yield less intense accelerating fields which are non-linear functions of the radial and longitudinal coordinates, contributing in increasing beam emittance; on the other hand, the former are more unstable but produce high, linear fields. Stronger fields mean a greater final energy but also a higher sensitivity to any jitter and on bunch mismatching. A good choice seems then to be right in the middle, exploiting a mildly non-linear regime. This choice comes from the need to prevent the possibility of self-injecting spurious charge, which can happen in the bubble regime, and exploiting, at the same time, the higher accelerating fields produced when the plasma wave is not linear. The plasma densities is then limited up to 1017 cm-3. The expected accelerating fields can then be estimated to be of the order of few tens of GV /m.
A major problem of the LWFA scheme is that, given a typical laser energy of a few Joules and a length of tens of fs, the condition on the laser intensity is met with a laser spot size of few tens of microns. For Gaussian pulses, such a value implies a Rayleigh length at most of few centimeters, which is surely not enough to produce a significant increase of the electrons energy. There are two main strategies for achieving guiding: either by transverse tapering of the plasma density or by using a capillary as an optical waveguide. Transverse tapering, though harder to properly manage, has the advantage of preventing any laser energy leakage from the plasma channel, allowing a longer acceleration; on the contrary, the capillary waveguide is easier to operate but, due to losses at the dielectric boundaries, allows acceleration lengths up to 6-8 cm (assuming a glass capillary) and severely constrains the laser spot-size w0 and focus position. We opted for the capillary waveguide, at least for the first part of the external injection experiment.
Extensive simulations performed using the code QFLUID2, a cylindrical code that uses fluid approximation and QSA for plasma currents and employing the transverse tapering guiding of the laser pulse, showed that it is possible to boost high brightness electron bunches energy with an accelerating gradient of 3 – 10 GV/m, preserving quality, at least at the slice level. A choice of 1017 cm-3 for plasma density is usually a good compromise between requirements on initial beam length and acceleration performances, while the capillary inner diameter is in the order of 100 µm. For preventing a huge normalized emittance dilution after the bunch leaves the plasma, a proper matching at plasma entrance end exit must be enforced. This can be done by properly tapering the plasma density ramps at both ends of the capillary. This feature also increases the overall scheme stability.
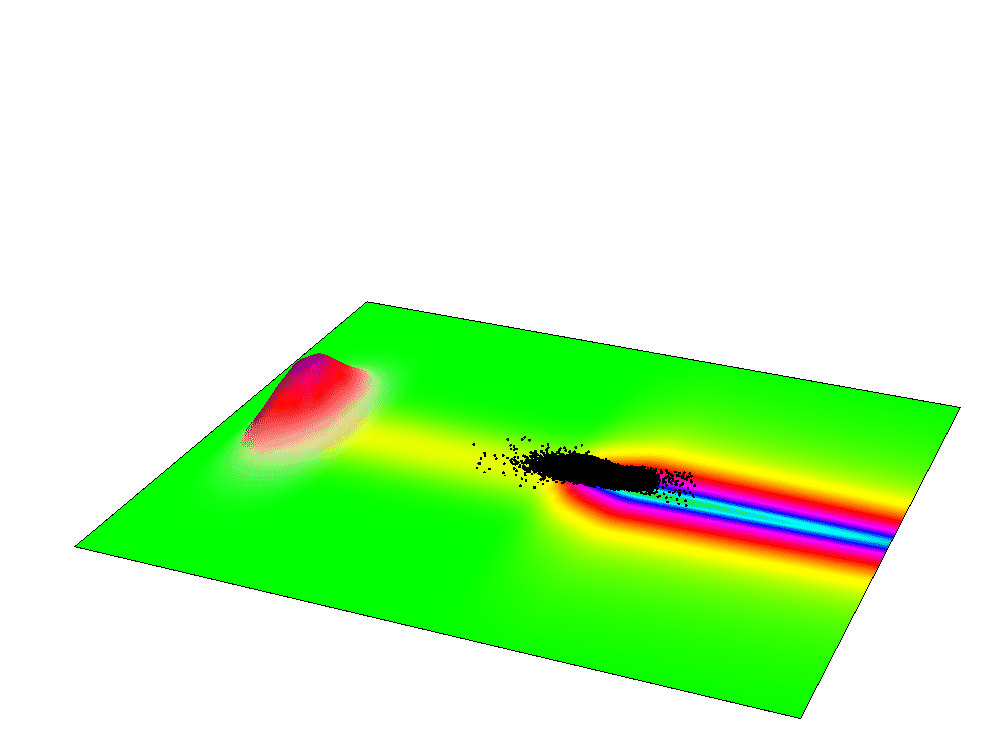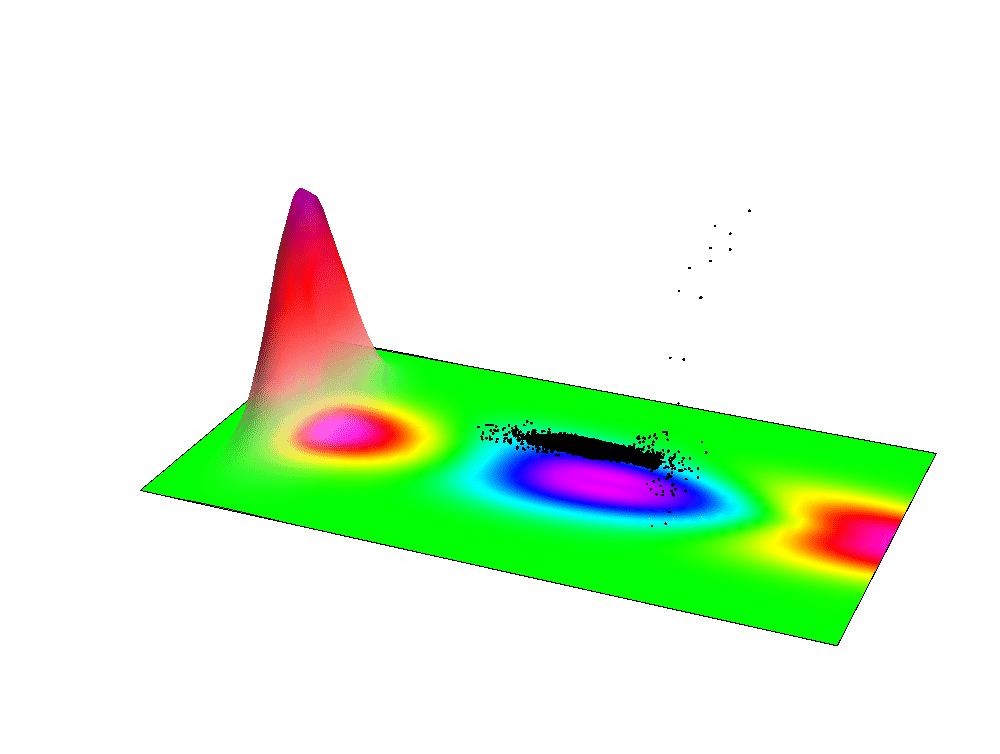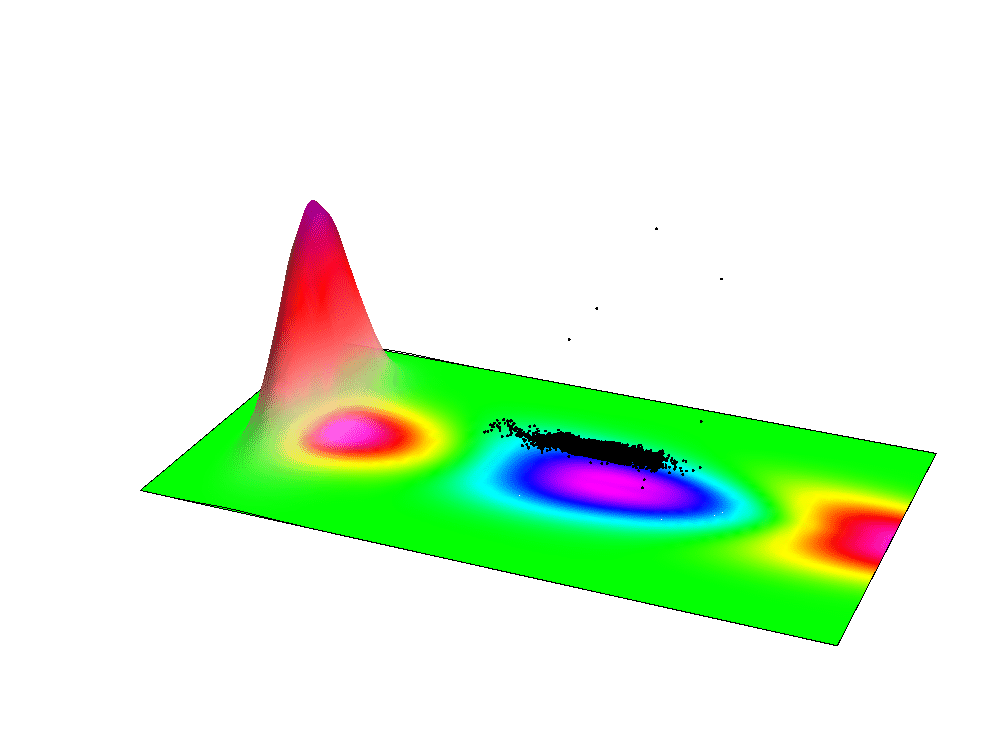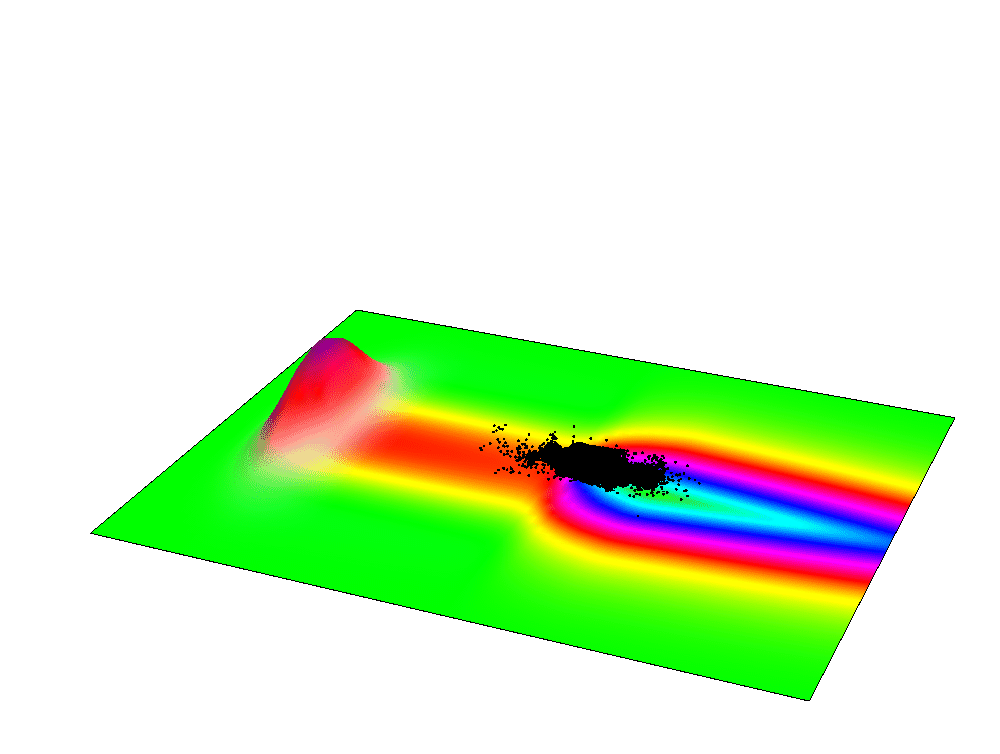
Simulation of the LFWA acceleration: the laser pulse is near the edge of the image, the accelerated electrons in the middle and the reference system is co-propagating with the beams.
Publication highlights:
- “Chromatic effects in quadrupole scan emittance measurements”, A. Mostacci et al., Phys. Rev. ST Accel. Beams vol. 15 (2012) pag. 082802, doi: 10.1103/PhysRevSTAB.15.082802
- “The External-Injection experiment at the SPARC_LAB facility”, A. R. Rossi et al., Nucl. Instrum. Meth. Phys. Res. A vol. 740 (2014) pag. 60, doi: 10.1016/j.nima.2013.10.063
- “Intrinsic normalized emittance growth in laser-driven electron accelerators”, M. Migliorati et al., Phys. Rev. ST Accel. Beams vol. 16 (2013) pag. 011302, doi: 10.1103/PhysRevSTAB.16.011302
- “Matching strategies for a plasma booster”, P. Tomassini and A. R. Rossi, Plasma Phys. Control. Fusion vol. 58 (2016) pag. 034001 doi: 10.1088/0741-3335/58/3/034001
- “Stability study for matching in laser driven plasma acceleration”, A. R. Rossi et al., Nucl. Instrum. Meth. Phys. Res. A vol. 829 (2016) pag. 67, doi: 10.1016/j.nima.2016.02.015
Plasma experiments
Last update 05/2019

